One of the reasons we started the Lance file format and have been investigating new encodings is because we wanted a format with better support for random access. Random access I/O has traditionally been ignored by columnar formats, and with reasonably good arguments...or at least, arguments that sound reasonably good. In this post we break down the old reasoning and explain why it falls short.
The case against random access
Let's start with the status quo which boils down to:
- Random access is slower
- Random access is more expensive
- If you want random access you're better off with a row-based format
That seems like a pretty solid case but it's not quite so simple. Let's break down each point in more detail.
Problem: Random access is slower
Random access is slower than linear access. This depends on the storage mechanism (NVME and RAM don't suffer too much) but it is exceptionally true for cloud storage. Cloud storage, by default, typically offers around 4-5 thousand IOPs per second per bucket. You can increase these limits in various ways but it isn't very easy, requires a lot of fine-tuning, and probably multiple instances. On the other hand, cloud instances can easily achieve 30-40Gibps or more of bandwidth. Fully profiling cloud storage is a difficult task but from just these numbers we can build a very rough rule of thumb:
These numbers aren't perfect. It's very hard to get 5GBps on cloud storage and sometimes we get more than 4K IOPs but they are probably within a factor of 2. The important part is the ratio. If we break this down that means we need to read 1MB per IOP to saturate the bandwidth (4K * 1M == 4G)! This suggests we can have quite a lot of read amplification and still get the same performance. Or, in parquet terms, if each data page is 1MB then we can afford to read an entire data page and still get the same throughput.
Rebuttal: Latency vs Bandwidth
The first thing to point out with this reasoning is that we are only looking at bandwidth. In cloud storage, even though we are limited in how many requests we can make, the latency of those requests decreases significantly as the request size decreases, all the way down to somewhere around 4 to 32KiB.
In other words, a cloud storage page-at-a-time parquet system and a random-access lance system might both be limited to the same searches per second (throughput) but the queries in the random-access system will have significantly lower latency than the queries in the page-at-a-time system, unless your data pages are 4KiB (not practical for current parquet readers but we might be moving Lance to use 4KiB pages for scalar types in the future 😉).
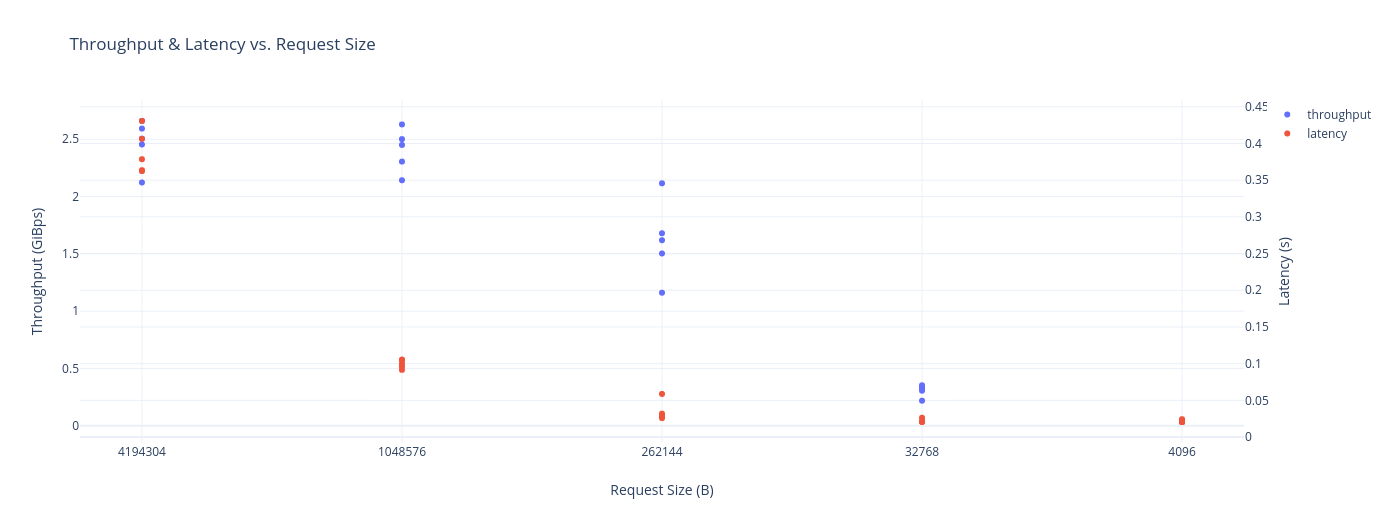
Rebuttal: Row size matters
Note the difference in units. 4K rows per second and 4B bytes per second. As I already pointed out, once a single row reaches 1MB the random access penalty is gone. Now, even with multi-modal data, we are unlikely to reach 1MB per row (unless working with video). However, it is not entirely uncommon to have something like 128KB per row (compressed images, HTML pages, source code documents, etc.) With rows this wide, the random access penalty is much smaller and the old rationales start to quickly fall apart. For example, modern parquet readers are starting to add late materialization for large columns because, suddenly, random access isn't so frightening anymore.
Rebuttal: Future proofing
The other problem here is that this logic is mostly predicated on a "cloud storage" way of thinking that has been around for quite some time. My personal prediction is that this IOPs per second limitation will be disappearing from cloud storage offerings in the future (possibly in the form of a "bulk get"). Even if it doesn't, data engineers can bypass these limits with their own services. In our enterprise product we already have caching layers that allow us to blast past this limitation. If you change the above analysis to be based on NVME instead of cloud storage it completely falls apart. As soon as your read amplification forces you to read from many (4KiB) disk sectors instead of a single disk sector then you are losing throughput.
Problem: Random access is more expensive
Another common refrain is that random access is more expensive. Once again, this reasoning is usually based in the cloud storage world. The classic reasoning basically boils down to "cloud storage charges per IOP and random access needs more IOPs". The typical use case considered is something like "SELECT x,y FROM table WHERE x IS TRUE" and we start to talk about things like "selectivity thresholds", "early materialization", and "coalesced I/O". For example, a common claim might be "if x is true 1% of the time then it is cheaper to scan the entire y column than it is to pick the values matching the filter using random access" and this is true.
Rebuttal: Selectivity thresholds don't always scale
The first problem here is that we're relying on this 1% selectivity threshold which means the # of rows that matches our filter scales with the dataset. This is important for the original argument. For example, if we select 10 rows from 1M potential rows there is a high chance we will coalesce. If we select 10 rows from 1B potential rows there is almost no chance we will coalesce.
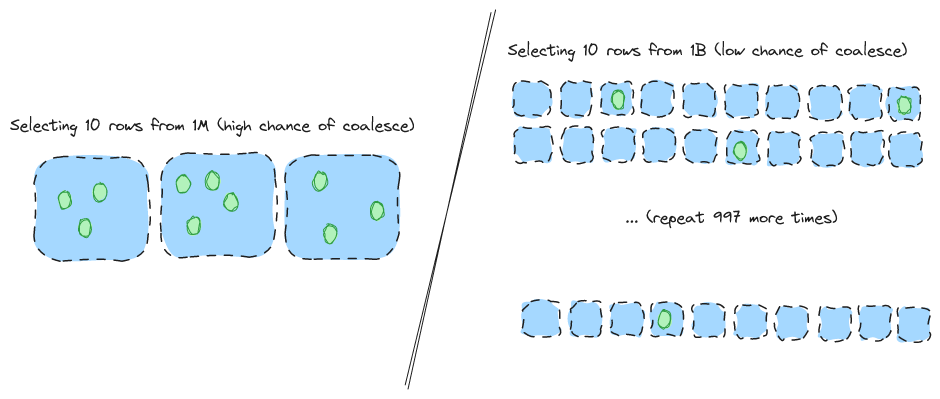
Of course, it seems obvious to assume that a filter scales with our data. However, there are many operations where the filter does not scale with the data. For example, workflows such as find by id, update by id, upsert, find or create, vector search and full text search all target a very narrow range of data that does not grow with dataset size. Existing formats struggle with these workflows because they rely on coalescing for random access instead of optimizing the random access itself.
Rebuttal: You can have your cake and eat it too
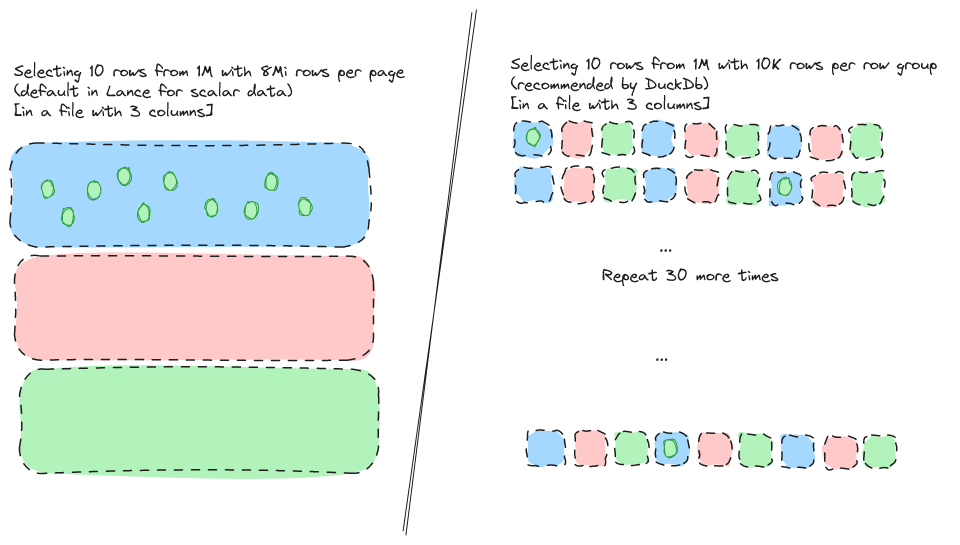
The second problem with the above argument is a simple one. We can absolutely coalesce I/O and support random access at the same time (Lance coalesces I/O within a page). In fact, I would argue that Lance is even more likely to coalesce I/O because its default page size is very large (8MiB).
Rebuttal: It costs CPU cycles to throw data away
The final problem with the cost argument is that it focuses on the I/O cost (cost per IOP) and ignores the CPU cost. For example, let's pretend we've stored 8GB of 8-byte integer data and used some kind of compression algorithm to drop that down to 6GB. Then, we want to select 1% of our data. We only want to return 80MB of data (10M values). However, we need to load and decompress 8GB of data.
To give you a basic idea I ran a simple experiment with the pyarrow parquet reader. This isn't as rigorous as I'd normally like since the pyarrow parquet reader has no way of pushing down selection vectors into the decode but it should give a rough rule of thumb. With Lance I randomly accessed 1,000 values of the l_partkey (an integer) column from a scale factor 10 TPC-H dataset. With parquet I fully read in the l_partkey column into memory (~60M rows, snappy compression, 30 row groups, 1MB page size). I then repeated this query 1,000 times (to remove initialization noise). The random access approach required 71B instructions. The full scan approach required 1.34T instructions (approx. 19 times higher CPU cost).
Or, to put this into dollars, if we assume a core speed of 4B instructions per second, and a core cost of $0.0000124/second (based on current pricing of a c7i.16xlarge instance) then we get about 4,544,000 random access queries per dollar and about 241,000 linear scan queries per dollar of CPU.
But aren't we paying more for I/O? And doesn't I/O dominate cost?
Not necessarily. As I mentioned above, we are coalescing I/O for random access in Lance. Another way to think of this is, in Lance, we throw away bytes after reading but before decompression. In Parquet we don't throw bytes away until after decompression (and, with pyarrow, after decoding) Both formats are using nice 8MiB pages and so we end up with a minimum of 30 IOPs per request. With 1,000 rows across 30 pages we are going to get a lot of coalesced I/O. In S3 we pay $0.0004 per thousand requests. Let's do a bunch of math to calculate the cost of 1000 queries.
| Format | CPU cost | I/O cost | Total cost |
|---|---|---|---|
| Parquet | $0.00410 | $0.0012 | $0.00530 |
| Lance | $0.00022 | $0.0012 | $0.00142 |
As explained above, as the scale of our dataset increases, the difference in price will only grow (assuming this is a case where our filter is independent of dataset size).
Problem: Just use a row-based format
The final argument against random access is that you're better off with a row-based format if you want random access. This is a pretty simple argument and it's not wrong. A row-major format is going to give you better access than a column-major format if you are querying multiple columns of data. However, it's not that simple.
Rebuttal: You probably want both
Most workflows, at least, most workflows we see at LanceDB, need both types of access. For example, an extremely common workflow is AI model training & inference. Researchers start with a big list of some large data type (e.g. images, or common crawl HTML pages, or prose documents). They slowly grow new columns of data onto that page doing analysis and extraction of the data (this is very much a columnar operation). This process can end up with thousands of columns. Using a row-based format would be awful for performance here.
Then, once the model is built, they need to run inference against the data, and now they suddenly want random access. These random access queries typically only load a small set of columns and its always the same set of columns (e.g. source image and caption). Suddenly we need to support random access patterns.
We could, of course, store two copies of the data. This has the obvious problem of doubling your storage costs but there is the less obvious problem in that it tends to greatly increase your data team's engineering costs to manage the complexities of two different storage solutions. This need for both is exactly why we aim to develop a format that can do both processes efficiently.
Rebuttal: Cake, eat it, keep it, do both
Once again, the second rebuttal is simply that you can support both access patterns with a single format. In Lance we've already developed a "packed struct" encoding that can be turned on, at will, to pack the fields in a struct (with all fixed length fields) into a row-based format.
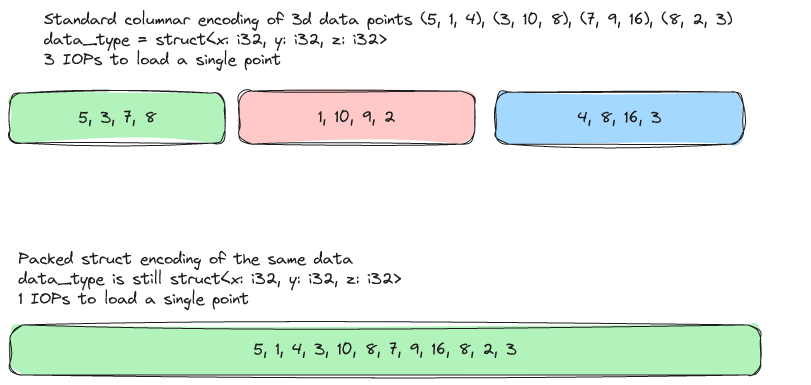
You can opt-in to this encoding on a per-struct basis using field metadata. This allows you to selectively pack fields that are frequently accessed together. In addition, we are planning a packed-row encoding which will allow you to pack together any set of fields (fixed or variable length) into a single variable-length data type. Once this is in place, we can even add a boolean flag to change the top-level encoding from columnar to row which would allow Lance to be used as a 100% row-based format.
This allows for simple and coarse grained switching between row & column formats as well as fine grained selection on a per-column basis. You can now fine-tune your format to maximize performance on any set of query patterns. If you really need both patterns for some columns then you can selectively duplicate those columns without creating a duplicate of all your other data (most importantly, avoiding duplication of expensive string and image data).
TANSTAAFL: Too good to be true?
Yes, it turns out we don't get everything for free. There are some legitimate drawbacks to support random access that we've encountered
- We plan on zipping definition and repetition levels with the values themselves, this has some small increase to repdef sizes since it means we cannot use RLE on the repdef levels (though we could potentially make use of it with the combined values). There's also a CPU cost associated with zipping and unzipping.
- In order to support random access we need to materialize null values (e.g. how arrow does it) instead of storing those arrays sparsely (e.g. how parquet handles it). Mostly sparse arrays will take up more space on disk (and thus more time to query).
- In order to support random access we can't support certain encodings (e.g. generalized block compression or delta encoding) which impacts our compressibility.
However, we believe many of these obstacles can be overcome. Clever use of run length encoding on values may tackle the first two bullet points for most real-world data sets (and there are ways we can do (mostly) random access with run length encoding 😎). Meanwhile, using small (4KiB) chunks for some data types can allow us to use encodings like delta without sacrificing random access performance. Or, we can find encodings like FSST which can give us compression without sacrificing random access.
These drawbacks have not been significant so far (indeed, we believe we make up for these drawbacks already with our smarter scheduling algorithms) and should only shrink with time as we get more sophisticated.
TL;DR:
- Random access has worse throughput on cloud storage but caching layers can avoid this and the improved latency is worth it in many situations.
- Supporting random access does not necessarily cost anything and can lead to cheaper and less CPU intensive workflows.
- The Lance format will eventually support both row and column storage patterns in a single format, giving your great flexibility in query patterns without adding to your development overhead or storage costs.



