Repetition and definition levels are a method of converting structural arrays into a set of buffers. The approach was made popular in Parquet and is one of the key ways Parquet, ORC, and Arrow differ. In this blog I will explain how they work by contrasting them with validity & offsets buffers, and discuss how this encoding impacts I/O patterns.
1. Parallelism without Row Groups
2. APIs and Fusion
3. Backpressure
4. Compression Transparency
5. Column Shredding
6. Repetition & Definition Levels (this article)
What Problem are we Solving?
Repetition levels are used when we need to convert a column into buffers. We discussed this briefly in the post on column shredding. In particular, we can look at three categories of columns: structs, lists, and primitives. Let's consider the following schema:
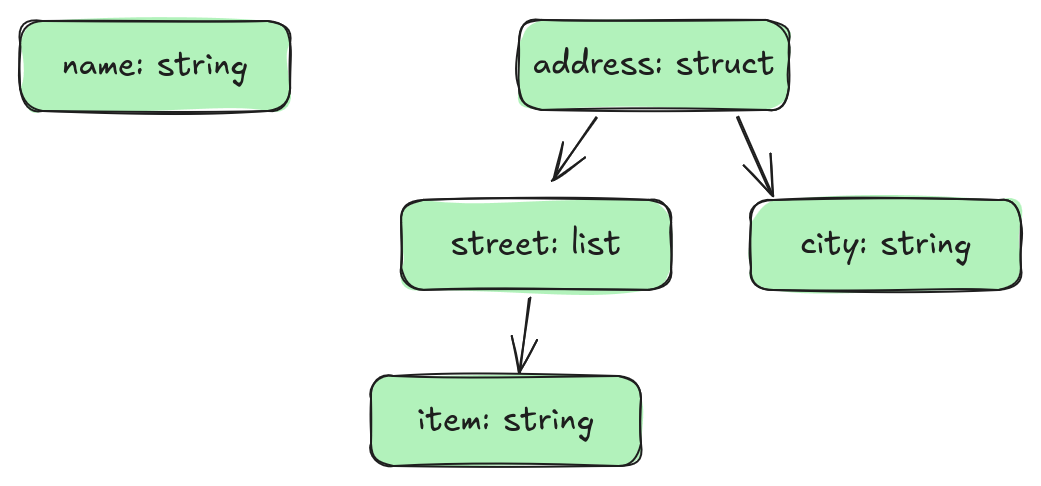
Let's gather some sample data:
- name: Reacher
address: null
- name: Herman Munster
address:
street:
- 1313 Mockingbird Ln
city: Mockingbird Heights
- name: Spiderman
address:
street: null
city: New York City
- name: Fry
address:
street:
- null
- Apartment 00100100
city: New New York
- name: Black Bolt
address:
street: []
city: ""We have two columns (name and address). Using the approach we described in the blog post on column shredding we need to turn this into arrays and buffers. We know, from that post, that we are going to transpose our data into leaf arrays (name, address.street, and address.city). However, there are a few details we have to consider:
- How do we express null values?
- How do we distinguish null values from null lists or null structs?
- How do we express lists as buffers?
How does Arrow Solve this Problem?
Arrow solves this problem with validity bitmaps and offsets arrays. Let's take a look at one possible representation of our sample data in Arrow. In order to make things interesting for those that know Arrow already, we'll exploit some idiosyncrasies.

1. There is a bit in the address.street.validity bitmap that is green. Why do you think that is? What's interesting about this bit?
2. The address.street.items.offsets array starts with 9. Is this legal? If so, why would this be allowed?
3. There is an easter egg in address.city.chars. Why doesn't this show up in our data? How could this happen in normal processing?
4. Where is address.city.validity?
Validity Buffers
Validity buffers tell us whether an item is null or not. Nearly all arrays in Arrow have a validity buffer. The validity buffer is optional. If an item is nested inside structs or lists you might need to look at ancestor validity buffers to know if the item is null or not.
![The top part is the data "outer: [ { "item": 5 }, NULL, { "item": NULL } ]. The middle row is the "outer.validity" buffer (101). The last row is the "item.validity" buffer (110)](https://blog.lancedb.com/content/images/2025/05/Validity-Buffers.png)
Offset Buffers
Offset buffers tell us how many items we have in each list when we have a list array. Empty lists are always a list of size 0. Nulls are usually a list of size zero. Arrow uses offsets, and not lengths, because this enables random access. To grab any single list we just need to look at the two offsets to determine the position in the items array.
![The top part is the data "lists": [[0, 3, 5, 7], [1, 3, 5], [], [2, 3, ]]. The middle part is the buffer "lists.offsets" 0, 4, 7, 7, 10. The bottom part is the buffer "lists.items" 0, 3, 5, 7, 1, 3, 5, 2, 3, 8](https://blog.lancedb.com/content/images/2025/05/Offset-Buffers.png)
Sharing is Caring but it Spreads Disease Data
In Arrow, validity and offset buffers are shared by nested children. This means there might be many leaf arrays that all share values from any single offset or validity buffer.
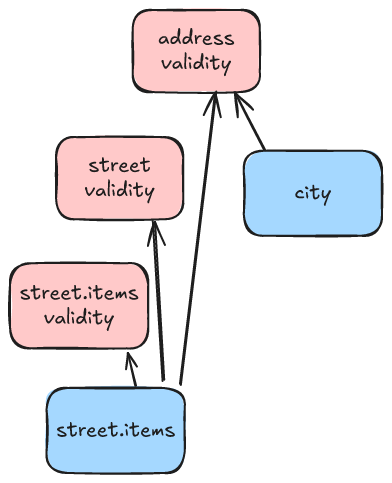
Sharing buffers like this is nice and compact and we avoid redundancy which is great if we want to change a value (e.g. mark an item null). However, it means we now have to look in several different locations to determine if an item is null. If our data is in memory that's usually fine. However, if our data is on disk, then this can become an impediment to random access.

Fortunately, we just saw a way to solve this in our previous post. We can zip the buffers together. Unfortunately, we can only do this if all the buffers have the same length. If we have lists, this probably isn't the case. So, we need to find some way to tweak our validity and offset buffers so they become zippable, and then zip them up. It turns out, if we do this, we can also take advantage of some redundancy to compress the buffers. This process gives us repetition and definition levels!
Repetition & Definition Levels
Repetition and definition levels, which I may just call repdef levels, are an alternate technique that can be used instead of validity and offset buffers. They solve the same problem, but in a different way. Why would we want to do this? Because, as we just described above, repdef levels are zipped together which can help random access.
Definition Levels Replace Validity Buffers
We will start with definition levels. These replace validity buffers. Let's start with a simple example where we have three levels of nesting giving us three validity bitmaps:
metadata.validity: [ 0, 1, 1, 1, 1 ]
metadata.user.validity: [ 1, 1, 0, 1, 0 ]
metadata.user.ip.validity: [ 0, 1, 0, 0, 1 ]To start with, we just zip our items up.
validity: [ 010, 111, 100, 110, 101 ]Or, visually:
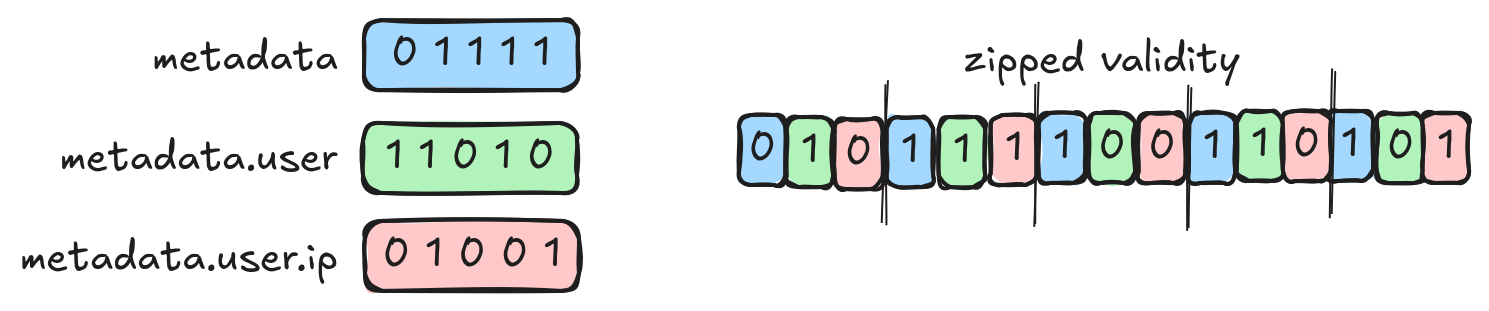
At this point, we're doing pretty good. We've got a single buffer. The validity bits for any particular row are next to each other. We will need 1 bit per level of nesting. That's not bad. However, we can do better. There's redundancy here and we can exploit it. Look in more detail at the third and fifth item of our example.
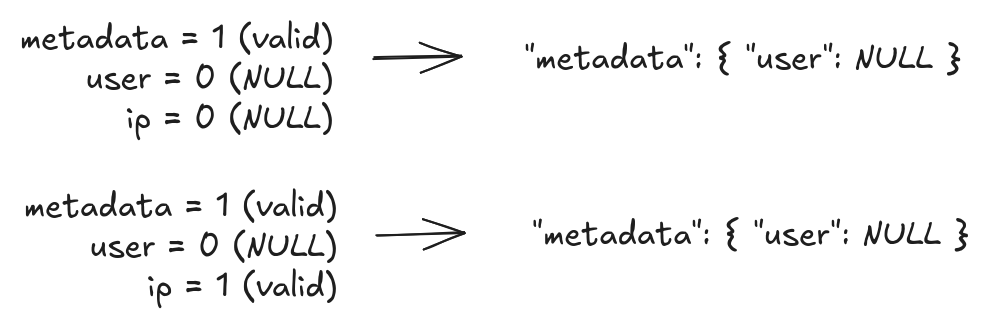
In the third item, both the user and ip validity bits are 0. We have a null user. In the fifth item the user validity bit is 0 but the ip validity bit is 1. However, we still have a null user. A null item can't have valid children. Once we encounter a null bit then the remaining bits are meaningless. In other words, after we zip three validity buffers, instead of the 8 possible values that we'd expect from a 3-bit sequence, we only have 4:
- Item is valid: 111
- ip is null: 110
- user is null: 10?
- metadata is null: 0??
Before, when we zipped these three levels, we needed three bits per value. However, if there are only 4 possibilities, we should only need 2 bits per value. We can assign any numbering scheme we want to these possibilities. In classic fashion, I picked the exact opposite scheme that Parquet picked 🤷 when I wrote this in Lance (I didn't read those repetition and definition tutorials in enough detail).
| Meaning | Definition Level (Parquet) | Definition Level (Lance) |
|---|---|---|
| Item is valid | max_def | 0 |
| Item is null | max_def - 1 | 1 |
| Parent is null | max_def - 2 | 2 |
| ... | ... | ... |
| Column root is null | 0 | max_def |
Putting it all together: We can convert N validity bitmaps into a single buffer of definition levels with log_2(N + 1) bits per value. Zipping and compressing at the same time.
Repetition Levels Replace Offsets
So now we have a way of handling validity buffers. Let's take a look at our offsets buffers. Remember, offset buffers tell us how many items we have in each list.
Lists: [ [0, 1, 2], [3, 4, 5] ], [ [6, 7] ]
Outer Offsets: 0, 2, 3
Inner Offsets: 0, 3, 5, 6, 8
Our goal is to get something that we can zip together with our items so we need it to have the same length.
Items : 0 1 2 3 4 5 6 7
Outer Repetition : * * * * * * * *
Inner Repetition : * * * * * * * *Were you able to figure it out? Perhaps there is more than one way?
Repetition bitmaps work by inserting a 0 whenever we start a new list and inserting a 1 whenever we are continuing the previous list.
Items : 0 1 2 3 4 5 6 7
Outer Repetition : 0 1 1 1 1 1 0 1
Inner Repetition : 0 1 1 0 1 1 0 1Again, more visually:
![There is a data array in the middle ([[0, 1, 2], [3, 4, 5]], [[6, 7]]). The top has a "Outer Repetition" buffer (01111101). The 0's point to the start of the outer lists. The bottom has an "inner repetition" buffer (01101101). The 0's point to the start of the inner lists.](https://blog.lancedb.com/content/images/2025/05/Road-to-Rep-Levels.png)
This is starting to look a lot like our definition bitmaps. We have a new bitmap for each level of repetition. Once again, there is the exact same redundancy that we can exploit. Whenever we start a new outer list we must start a new inner list at the same time, and so the lower level bits don't matter when the high level bit is zero. I'll skip a few steps because the conclusion is the same. We combine all of our bitmaps into a single buffer of levels. Once again, Lance and Parquet completely disagree on what order we should use 😇
| Meaning | Repetition Level (Parquet) | Repetition Level (Lance) |
|---|---|---|
| No new list | max_rep | 0 |
| New innermost list | max_rep - 1 | 1 |
| ... | ... | ... |
| New outermost list | 0 | max_rep |
Putting it All Together
Let's assume we have a column of tests which is a struct that has an item cases which is a list of structs and those structs have a field points which is a list of structs and those structs have fields x and y and we want to decode the leaf field x. Here is one example record:
tests:
cases:
- points:
- x: 7
y: 3
- x: 2
y: 4
- points:
- x: 0
y: 0Ok, now let's work backwards and test our skills. Let's look at just the column x and look at some sample items and repetition and definition levels:
items : 0 1 2 3 4 5
repetition : 0 2 0 0 1 2
definition : 4 4 0 1 2 3Can figure out the original document? First, in order to interpret our levels, we actually need to know the schema and nullability of the document. This is because we don't want to waste a precious repetition or definition slot when we know a particular level is non-nullable.
For our example we will assume that both of our structs can be null, as well as our value. However, we have no null lists. We also need one level for "valid item". Next, we know there are two lists and we need one level for "does not start new list". Putting this together we get:
| Level | Definition Meaning | Repetition Meaning |
|---|---|---|
| 0 | Null test | New list of cases |
| 1 | Null case | New list of points |
| 2 | Null point | No new list |
| 3 | Null x | - |
| 4 | Valid item | - |
At this point it should be a straightforward exercise to construct the original representation. I encourage you to give it a try.
Click for the answer
- tests:
cases:
- points:
- x: 0
- x: 1
- null
- tests:
cases:
- null
- points:
- null
- x: nullNull Stripping?
In the previous example I included garbage values for nulls. Note that the items array has 2, 3, 4, and 5 but those numbers don't appear anywhere in the answer. If we want our repetition and definition levels to line up with our values so we can zip them then we do need some kind of dummy value. However, this isn't a requirement for repdef levels. You could completely reconstruct the above array without having those dummy values. In fact, Parquet always strips out null values.
Empty / Null Lists?
I've intentionally avoided empty & null lists in my examples. Let's look at them now. Null lists are pretty straightforward. They are a "new list" of sorts so we will use our list repetition level. They are null so we will reserve a definition level.
Now let's look at an empty list. They are also a "new list" of sorts so we will use our list repetition level. However, what should we use for the definition level. If we use the same we used for nulls then they show up as a null list. If we use the definition level for "valid item" then we will try and add an item to the list and that isn't right either.
![The top is the data ([5], NULL, [], [6]). The left has our values buffer (5, 6), our Rep levels (0, 0, 0, 0) and our def levels (2, 0, 1, 2). A caption points to the rep levels that says "Rep level is always 0 since we always start a new list in our data". There is another caption pointing to the def levels that says "Def level is needed to distinguish between NULL and []"](https://blog.lancedb.com/content/images/2025/05/Rep-Levels-Empty-Null-Lists.png)
It turns out that empty lists also need to reserve a definition level. This means a list array that has both empty lists and null lists will take up two definition level spots.
Why Do We Care?
We now have two completely different ways to convert struct and list arrays to a set of buffers. The Arrow (validity & offsets) approach and the RepDef (repetition & definition) approach. How do these two approaches compare?
Both can be compressed. Repetition levels and definition levels are naturally compressed as they are created. They can be further compressed with run length encoding (this is done in Parquet) which is often useful as it is common to have only a few nulls in an array.
However, validity buffers can be compressed as compressed bitmaps (e.g. roaring bitmaps is one approach) and offsets buffers can be bitpacked and possibly even delta encoded for compression. In fact, I would wager it's pretty difficult to pick one approach over the other purely based on compression (though it would be an interesting study if anyone knows of one).
Offsets support random access. If you have an offsets array then you can access the Nth list in O(1) time. If you have repetition levels you have to search the repetition levels until you find the Nth instance of your desired level. This requires O(N) time.
Validity buffers are a single source of "physical" truth. If you have validity buffers then you have one source of truth for "physical validity" (the validity of a single level). If you need to mark a struct as NULL you can do that by changing one bit in one buffer. With definition levels, to mark a struct as NULL, you need to change the level buffer of every child.
Definition levels are a single source of "logical" truth. If you have validity buffers then you need to read multiple buffers to figure out if a value is "logically NULL" (e.g. is this NULL or any of its parents?) With definition levels you only need to read a single spot.
Repdef Levels are not "zero copy". Like many techniques used in file storage (compression, zipping buffers, etc.) there is a cost to pay. Repdef levels are no exception. In order to convert the data back into Arrow format we must pay a conversion cost to "unravel" the repdef levels back into validity & offset buffers.
Why does Lance care?
The reason I got interested in repetition and definition levels, while working on Lance, is because repetition levels and definition levels are single buffers that can be zipped together. With repetition and definition levels the number of buffers any single leaf array has remains relatively small. This is useful for random access as it keeps our data closer together instead of spread out all over the place. However, the lack of an offsets buffer does present a challenge for random access, something we will tackle in the next post.
In fact, at this point, we've now covered several techniques that come to similar conclusions. Transparent compression, buffer zipping, and repdef levels are all tradeoffs between CPU costs and random access performance. In the next post, which will cap this recent sequence of posts, we will look at the concept of structural encoding. This ties all these posts together and shows how Lance decides between these various techniques.
LanceDB is upgrading the modern data lake (postmodern data lake?). Support for multimodal data, combining search and analytics, embracing embedded in-process workflows and more. If this sort of stuff is interesting then check us out and come join the conversation.




